Diferenciabilidad y continuidad.
Objetivo
El objetivo de este blog es ayudar y recopilar información para aquellas personas que estén necesitando ayuda en temas de matemáticas administrativas.
| Derivada; Diferenciabilidad La derivada de una función f en el punto a en su dominio se define por
Diferenciable en un subconjunto del dominio La función f es diferenciable en el subconjunto S de su dominio si es diferenciable en cada punto de S. Nota
 |
Ejemplo 1 Funciones no diferenciables en puntos aislados
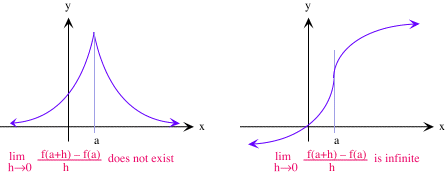Determina los puntos de no diferenciabilidad de las siguientes funciones
| (a) | f(x) | = | (x-1)1/3 | (b) | g(x) | = | |x+2| | (c) | r(x) | = |  x - 1 |
Solución
(a) La regla de la potencia nos dice que f(x) = (x-1)1/3 tiene derivada f'(x) = (1/3)(x-1)-2/3 en todas los puntos donde se define esta expresión, y no es diferenciable cuando (1/3)(x-1)-2/3 no se define. Porque (x-1) tiene un exponente negativo, f'(x) no está definido cuando x = 1, y por lo tanto f no es diferenciable ahí. De hecho, un cálculo directo muestra que
| lim h  0 | h | = | lim h 0 | h | = | lim h 0 | h2/3 | = | + , |
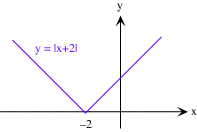
| (b) | Porque g(x) = |x+2| = |  | -(x+2) x+2 | si x  -2si x > -2 | , |
y que ya sabemos que los -(x+2) y x+2 son diferenciables, el único punto en el que puede salir algo mal es cuando x = -2. En este punto, podemos calcular el límite del cociente de la diferencia directamente:
| lim h 0 | h | = | lim h 0 | h | . |
(c) La regla del cociente nos dice que r(x) = x2/(x - 1) es diferenciable en todos los puntos excepto en x = 1. Sin embargo, x = 1 no está en el dominio de r, y por lo tanto r es diferenciable en todos los puntos de su dominio.
Como vemos en la gráfica a la derecha, no hay puntos de tangencia vertical o cúspides.
Antes de seguir...
Como se puede ver, las gráficas proporcionan información inmediata en cuanto a dónde debe buscar un punto de no diferenciabilidad: un punto donde parece que hay un cúspide o una tangente vertical.
Aquí está uno para ti.
Ejemplo 2 Puntos de no difereciabilidad
P En Parte A hablamos de continuidad, y aquí hablamos de diferenciabilidad. ¿Son todas las funciones continuas son diferenciables? ¿Todas las funciones diferenciables son continuas?
R Brevemente:
(a) No todas las funciones continuas son diferenciables. Por ejemplo, la función de forma cerrada f(x) = |x| es continua en cada número real (incluyendo x = 0), pero no diferenciable en x = 0.
(b) Sin embargo, cada función diferenciable es continua. Más precisamente, tenemos el siguiente teorema.
R Brevemente:
(a) No todas las funciones continuas son diferenciables. Por ejemplo, la función de forma cerrada f(x) = |x| es continua en cada número real (incluyendo x = 0), pero no diferenciable en x = 0.
(b) Sin embargo, cada función diferenciable es continua. Más precisamente, tenemos el siguiente teorema.
Teorema Diferenciabilidad implica continuidad
Si f es diferenciable en a, entonces es continua en a.
Prueba
Supongamos que f es diferenciable en el punto x = a. Entonces sabemos que
Supongamos que f es diferenciable en el punto x = a. Entonces sabemos que
| lim h 0 | h | existe, e igual f'(a). |
| lim h 0 | f(a+h) - f(a) | = | lim h 0 | h | . h | = | f'(a). 0 = 0. | Límite del producto = producto de los límites |
| lim h 0 | f(a+h) | = | lim h 0 | [f(a+h) - f(a)] + f(a) | = | 0 + f(a) = f(a). | Límite de la suma = suma de los límites |
| lim x-a 0 | f(x) | = | f(a). |
| lim x a | f(x) | = | f(a), |
Ahora puedes probar el resto de los ejercicios en los ejercicios para este tema.
Bibliografía:
0 comentarios:
Publicar un comentario