2.4 Límites al infinito.

Límites al infinito.

Objetivo
El objetivo de este blog es ayudar y recopilar información para aquellas personas que estén necesitando ayuda en temas de matemáticas administrativas.

Uno entre infinito

Empecemos por un ejemplo interesante.

Pregunta: ¿Cuál es el valor de 1/∞ ?

Respuesta: ¡No lo sabemos!

¿Por qué no lo sabemos?

La razón más simple es que infinito no es un número, es una idea. Así que 1/∞ es un poco como decir 1/belleza o 1/alto.

A lo mejor podríamos decir que 1/∞ = 0 ... pero eso es un poco problemático, porque si dividimos 1 en infinitas partes y resulta que cada una es 0, ¿qué ha pasado con el 1?

De hecho 1/∞ es indefinido.

¡Pero podemos acercarnos a él!

Así que en lugar de intentar calcular con infinito (porque no sacaremos ninguna respuesta razonable), vamos a probar con valores de x más y más grandes:

x 1/x 1 1.00000 2 0.50000 4 0.25000 10 0.10000 100 0.01000 1,000 0.00100 10,000 0.00010

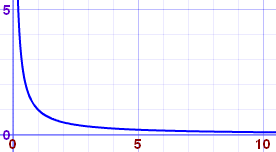Vemos que cuando x crece, 1/x tiende a 0

Ahora tenemos una situación interesante:

• No podemos decir qué pasa cuando x llega a infinito
• Pero vemos que 1/x va hacia 0

Queremos decir que la respuesta es "0" pero no podemos, así que los matemáticos usan la palabra "límite" para referirse exactamente a esto

El límite de 1/x cuando x tiende a infinito es 0

Y lo escribimos así:

En otras palabras:

Cuando x va a infinito, 1/x va a 0

Cuando veas "límite", piensa en "acercarse"

Es una manera matemática de decir que "no estamos hablando de lo que pasa cuando x=∞, pero sabemos que cuando x crece, la respuesta se acerca más y más a 0".

Resumen

A veces podemos no usar infinito directamente, pero sí podemos usar un límite.

Lo que pasa en ∞ es indefinido...	1/∞
... pero sabemos que 1/x va hacia 0 cuando x va hacia infinito

Límites al ir a infinito

¿Cuál es el límite de esta función?

y = 2x

Está claro que cuando "x" se hace más grande, le pasa lo mismo a "2x":

x	y=2x
1	2
2	4
4	8
10	20
100	200
...	...

Así que cuando "x" va a infinito, "2x" también va a infinito. Lo escribimos así:

Pero no te dejes engañar por el signo "=". No podemos llegar a infinito, pero en el lenguaje de los "límites", el límite es infinito (lo que quiere decir en realidad que la función no tiene límite).

Bibliografía: http://www.disfrutalasmatematicas.com/calculo/limites-infinito.html